Bus Routing Problem

For my Bachelor's thesis, students were assigned a general topic to use. In my case, this was the Vehicle Routing Problem (VRP). Instead of applying a new method to an existing variant of the VRP, I figured it would be fun to come up with a new variant and solve it. I spent some time staring out the window of my student room, trying to think of an exciting vehicle-related challenge. I think about half a dozen buses must have driven by before I realized the universe was trying to tell me that they were the perfect topic to study.

Solution Problem based thinking

In most assignments during my time at Tilburg University, we would be given a problem and then be asked to solve it. It was therefore a fun and new experience to actually design a problem myself, starting from scratch.

There are many different aspects of urban bus networks that could have been interesting to analyze. For example, I could have tried planning a timetable for given bus routes, or determining the optimal places for new bus stops. In my thesis, I chose to limit the scope to the design of the routes the buses should follow. The problem was therefore named the Bus Routing Problem (BRP).

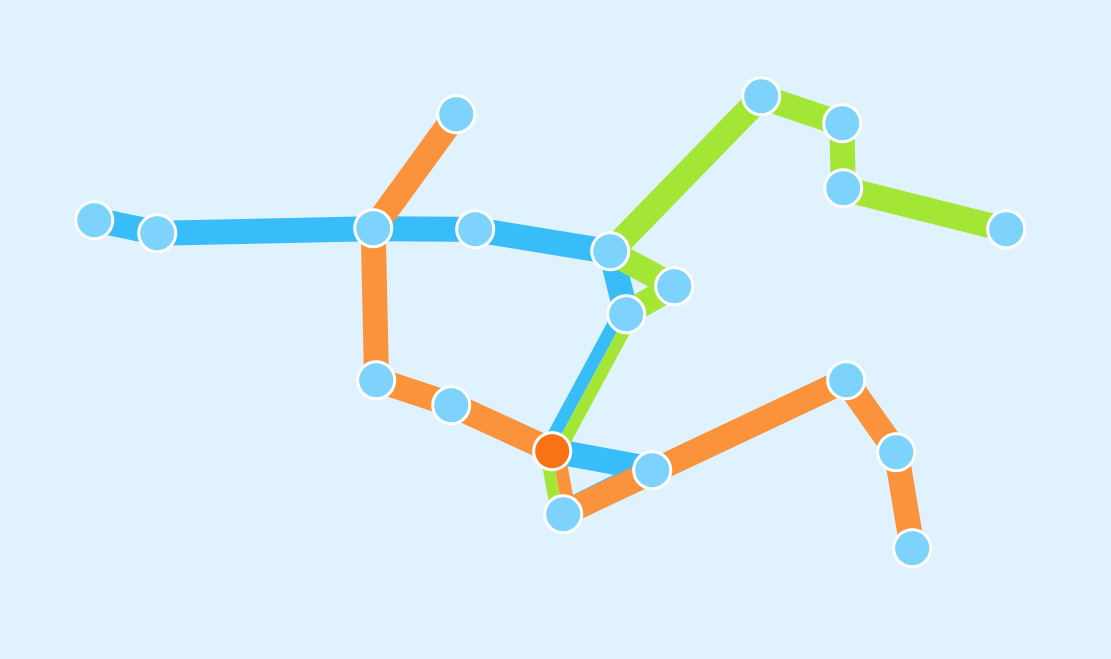
An instance of the BRP is defined by a set of bus stop locations, and a prespecified number of bus routes to draw. The following map shows what an instance might look like. Every dot represents the location of a bus stop, with the orange dot identifying the central bus station.

If you're familiar with Vehicle Routing Problems, then you'll notice this map is similar to those used in existing VRP variants. There are, however, a few differences in how routes should be drawn in the BRP compared to the VRP.

1. Every bus route has to visit the central station, but it does not need to start or end there.
2. Bus routes are not loops - they start and end at different locations.
3. Every bus stop location may be visited by any number of bus routes (at least 1).

A solution to the example could therefore look as follows (assuming the prespecified number of bus routes to draw is 3).

Evaluating a bus network

Take a look at the following two solutions to the same instance. Which solution would you consider as the best bus network of the two?

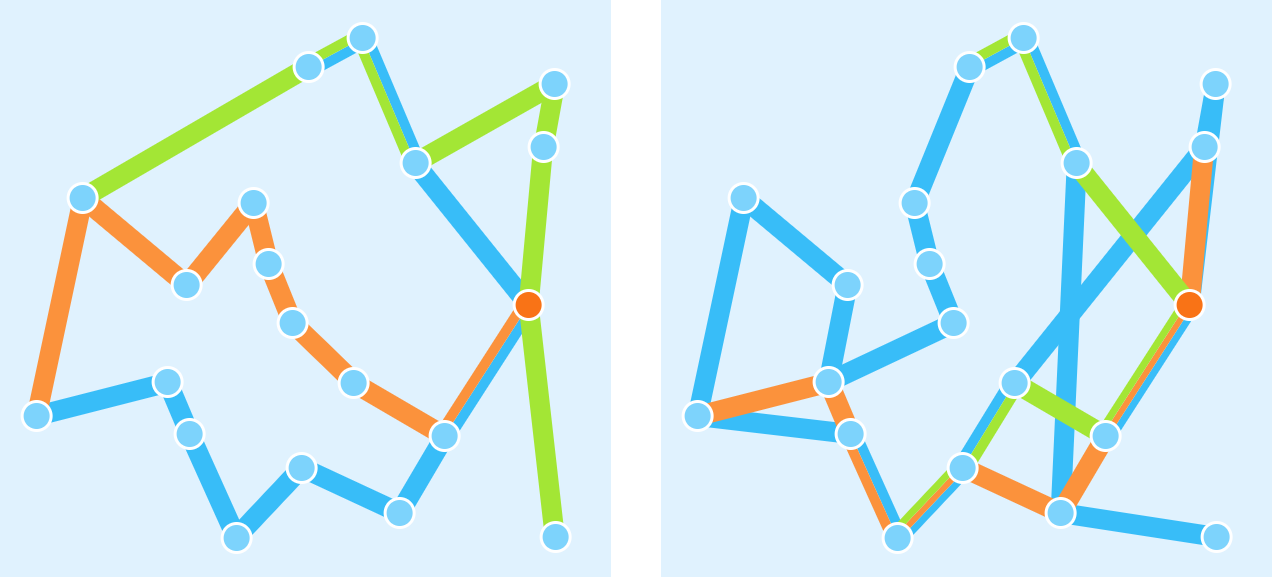
You might be inclined to prefer the bus network shown on the left. It looks more organized, and more alike bus networks we might find in real life. What we need, however, is a way to quantify the performance of any bus network - only then can we truly compare solutions and conclusively say which is deemed to be better. Choosing how solutions are evaluated was therefore one of the most important parts of designing the BRP.

I decided that the evaluation of a bus network should be done from the perspective of the passengers that are going to use it. Every passenger has a desired trip that they want to make (from some starting bus stop to a destination bus stop), and they want that trip to be possible using the bus network. Let me rephrase that: they want the bus network to be a viable option.

Whether taking the bus is viable is quite subjective, however. For some passengers this might depend on how crowded the bus will be, or how many times they have to make a transfer to another line. In my thesis, I defined viability as a condition on the total travel time.

The precise definition of viability is given below. Here, $t$ refers to a trip, with $v(t)$, $D(t)$ and $w(t)$ respectively referring to the viability, travel duration (using the bus network) and direct distance of trip $t$. The constant $c$ is chosen by preference. In my thesis, I used $c = 2$.

What this means is that taking the bus is considered to be a viable option if your travel duration is at most twice the time it would take you to drive there yourself. So, if going by car would take 15 minutes, the bus may take at most half an hour to get there. The goal of our bus network then becomes to maximize the number of viable trips, $\sum_{t} v(t)$.

Boarding and transferring

Now, we're ready to encounter the main challenge of designing this problem: what is the actual travel duration $D(t)$ of any given trip $t$, and how can we efficiently compute it? Consider the following bus network, and let's say you need to travel from bus stop 16 to the Central Station. It seems that taking the green line north would be the fastest way.

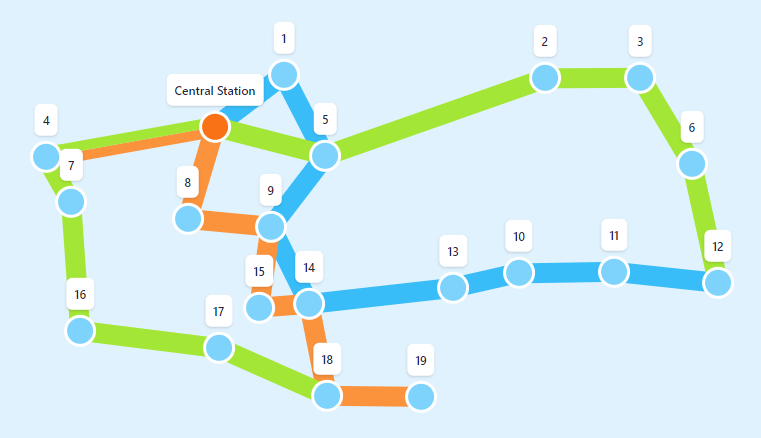
A more difficult question would be how you should travel from location 3 to location 18. If the goal is simply to achieve the smallest distance travelled, then you should transfer from the green onto the blue line at stop 5, and onto the orange line at stop 14.

However, if you've travelled by bus before then you'll know that the shortest path is not necessarily the quickest. Perhaps the connection between the blue and green line at stop 5 isn't that great, and transferring takes a lot of time. In that case, it might be faster to transfer to the orange line at the Central Station, or maybe to simply stay on the green line for the entire trip!

The delay caused by transferring to another line should definitely be included in the computation of travel time. But since timetables were left out of the problem's scope, they cannot be computed exactly.

I tried some different ways of accounting for these delays, and ended up introducing a boarding penalty that is incurred every time you board a bus line.

Finding all shortest trips

To be continued..

See it in action!